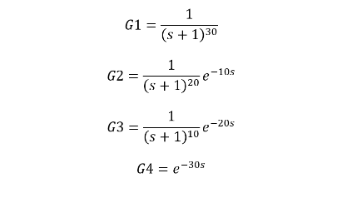A colleague commented: “In first-order lag processes, it’s easy to establish a quantitative relationship and draw conclusions with PI parameters, then extend these conclusions to higher-order processes. However, the issue is that thermal power control rarely involves first-order lags, and improving disturbance rejection is particularly critical for thermal power systems. Higher-order controllers exhibit significant performance differences between higher-order processes and first-order lag processes, rendering some conclusions derived from first-order lags and PI control inapplicable.”
The more fundamental question is: Is it necessary in industrial settings? Is this a widespread issue or a special case? What are the primary contradictions and their key aspects in on-site control? Is it truly a limitation of PID capabilities?
Pure time delays in controlled objects consist of two components. If the delay is caused by true transport delay, feedback control theoretically cannot eliminate it. However, if the pure delay stems from higher-order capacitive lags, a higher-order controller could theoretically mitigate it. This is a critical perspective for research into higher-order control algorithms.
In practice, however, distinguishing the cause of pure delays in a factory setting is challenging. Within a feedback control framework, using PI control to address the dominant time constant’s impact often suffices to achieve adequate disturbance rejection and fast response. If performance remains suboptimal, enhancements like cascade control, feedforward control, or structural modifications can be considered. Alternatively, efforts can focus on eliminating disturbance sources or improving the controlled object’s characteristics.
In most cases, precise modeling of the controlled object to enhance performance is neither practical nor necessary. Single-loop PI control dominates in factories, and for frontline engineers, parameter tuning is far more critical than adopting higher-order algorithms. Persistent control challenges on-site are better addressed through control scheme design and process improvements. Relying on unfamiliar algorithms often leads to suboptimal outcomes. Control algorithms that heavily depend on precise knowledge of the controlled object’s characteristics lack robustness in industrial environments, where uncertainties, unknown disturbances, and diverse constraints are ubiquitous. Advanced algorithms that ignore factory realities struggle to gain traction.
Many low-order forms of higher-order controllers are essentially variations of PI control. PI control is to feedback control what salt is to cooking—essential, while other elements are supplementary flavors. Devices relying heavily on feedback control indicate significant uncertainties, nonlinearities, and conflicts with process requirements. While precise modeling and process equipment upgrades could meet these requirements, cost considerations often favor feedback control if it achieves the desired outcome. The prevalence of feedback control in process industries highlights the significant uncertainties and nonlinearities inherent in these systems. Complexity is avoided unless necessary, which is why feedback control is less common in discrete manufacturing.
 |
Closed-Loop Step Response Curves with Lambda Tuning |
Consider four controlled object models analyzed using the Lambda tuning method. The time to reach 63.2% of the process variable change (ΔPV63.2%) is roughly similar, with T+τ around 30 seconds for each. However, the actual characteristics of these objects differ significantly. Their transfer functions are as follows: [Insert transfer functions if provided]. Attempting precise modeling of these objects is costly and often infeasible on-site. Crucially, near-equivalent control performance can be achieved without detailed knowledge of these model parameters.
The Lambda tuning method’s control results demonstrate this. PI control focuses on addressing the primary contradictions and their key aspects in the controlled object, leveraging feedback and PI tuning to achieve most performance improvements while using robustness to counter model uncertainties. The marginal performance gains from more complex control algorithms are often outweighed by the impact of uncertainties and model mismatches, making them less cost-effective.
The Lambda tuning method prioritizes simplicity, focusing solely on PI tuning to make it accessible for engineers and scalable across applications. For frontline engineers, PI control is sufficient in most scenarios. Special cases exist, but those are for scientists and specialists to address. Just as Newtonian mechanics suffices for everyday engineering despite the rigor of relativity, PI control remains practical and effective. As Wang Anshi wrote, “What seems ordinary is most profound; success appears easy, yet is arduous.”
 |
Comparison of Closed-Loop Step Response with Lambda Tuning |